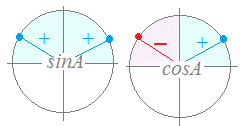
三角関数の相互関係 象限 280247

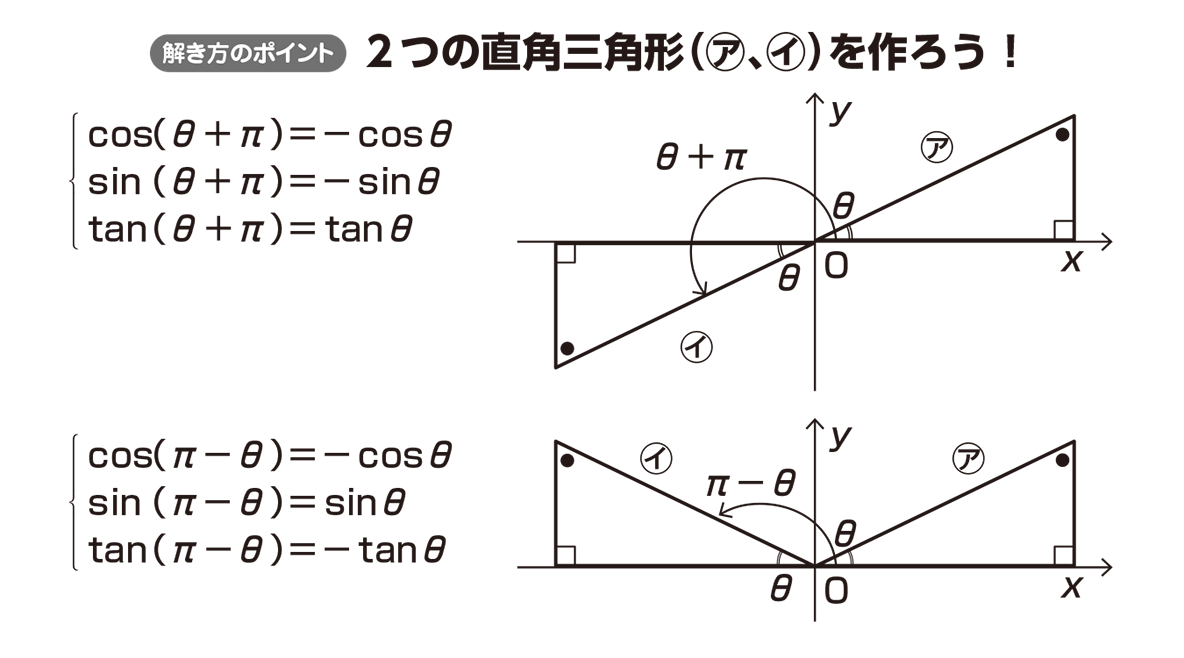
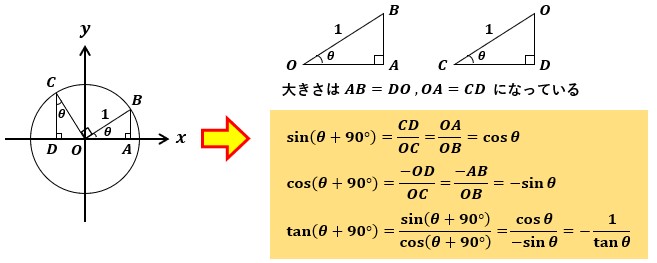
ピタゴラスの定理 や オイラーの公式 などから以下の基本的な関係が導ける 。 cos 2 ⁡ θ sin 2 ⁡ θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1\!} ここで sin2 θ は (sin (θ))2 を意味する。 この式を変形して、以下の式が導かれる： sin ⁡ θ = ± 1 − cos 2 ⁡ θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^ {2}\theta }}}次の問いを通して，三角比の相互関係を考えます 1 次の問いに答えましょう (1) 0° ≦ θ ≦ 180° で sinθ = 3 5 を満たすとき， cosθ と tanθ の値は？ (2) θ が第2象限の角で tanθ = − 2 を満たすとき， sinθ と cosθ の値は？ 2 0° ≦ θ ≦ 180° で定義された関数 f(θθπ/2ということは、θから π/2 移動した場所に三角形が来ることを表しますね。 π/2=90° なので、直角三角形アは 第2象限 の直角三角形イに移動します。

高校数学 8 と 8 P 8 Pの関係 映像授業のtry It トライイット

三角関数の相互関係 象限

三角関数の相互関係 象限-高校数学Iで登場する「三角比の相互関係」とは、次の2つの公式のことです。 sin 2 Acos 2 A=1 (1)三角関数の相互関係を利用して，一般角θのsinθ，cosθ， tanθをもう一度求めてみましょう。 学習のポイント 1三角関数の相互関係の特徴 2角の象限と三角関数の値の符号 3三角関数の相互関係の公式を利用する注意点 講師：元東京都立高校教諭 水谷 信也

三角関数

でも関数関係の扱いは可能であるから三角関数 という概念を導入することは数学Ⅰでも可能で あるという主張もなされる。提案の趣旨は，直 角三角形にこだわるのか，関数関係にこだわる のかということである。 さらには座標の導入は中学校でなされているθが第3象限の角で、 のとき、 、 の値 を求めよう!!兵 INて る (2) のが第2象限の角で, Dr S 。 思 237 三角関数の相互関係 次の値を※めょ。 *%1) ーー のとき, cosの, tan@ 3 (2) cosのテー計 のとき, sin@ tan9 *%3) tanの王2 のとき, sinひ cos0

1 tan2 = 1 cos2 3個目の1 tan2 = 1 cos2 は、1個目、2個目のsin2 cos2 = 1;53 三角関数の基本公式 (1) 三角関数の相互関係 式(51)より，三角関数には次のような関係が成り立ち，θの象限と，sinθ，cosθ， tanθ のいずれか1つの値がわかれば他の三角関数の値がわかる． tanθ = sinθ cosθ (52) sin2 θ cos2 θ = 1 (53)．三角関数 10時間(本時はその第3 時) 2 ．加法定理 5 時間 6． 教材観 数学Ⅰで学んだ三角比を一般角θまで拡張し，三角比の性質，θの動径の象限を理解 した上で三角関数の相互関係を用いた問題を解けるようにする。 7． 生徒観

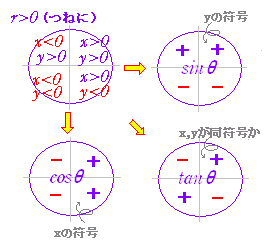
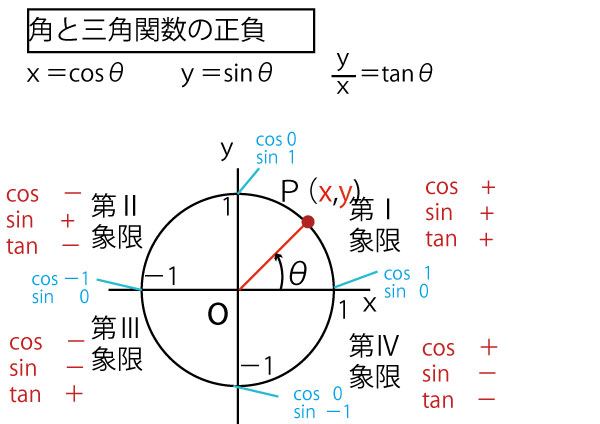
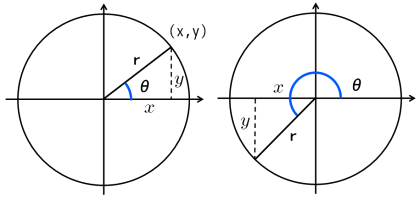
三角関数の相互関係 図10のような直角三角形においては，ピタゴラスの定理（三平方の定理）により， x 2 y 2 = r 2 が成り立つ． x ， y が負の場合にも，点（ x ， y ）と原点との距離の公式から， x 2 y 2 = r 2 がいえる． この式の両辺を r 2 で割ると = 1この等式も相互関係の1つである。 角の象限と三角関数の値の符号 y sinθ O x ＋ － ＋ － y cosθ O x － － ＋ ＋ y tanθ O x － ＋ ＋ － 三角関数の相互このページでは，はじめに， sin ( α β) ， cos ( α β) などの （ ）をはずす公式 「三角関数の加法定理」 を解説し，その応用として 「2倍角公式」「3倍角公式」「積和の公式」「和積の公式」 を解説する． (1) (2)の証明･･･ （以下の証明は第1象限の場合についてのものであるが，この公式は， α ， β が任意の角の場合でも成立する．） 右図において， ∠ AOB= α

三角比の相互関係

3

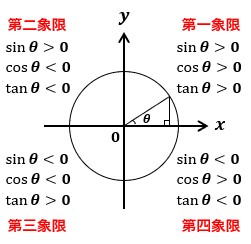
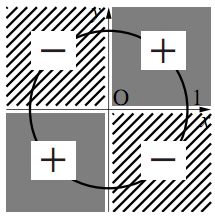
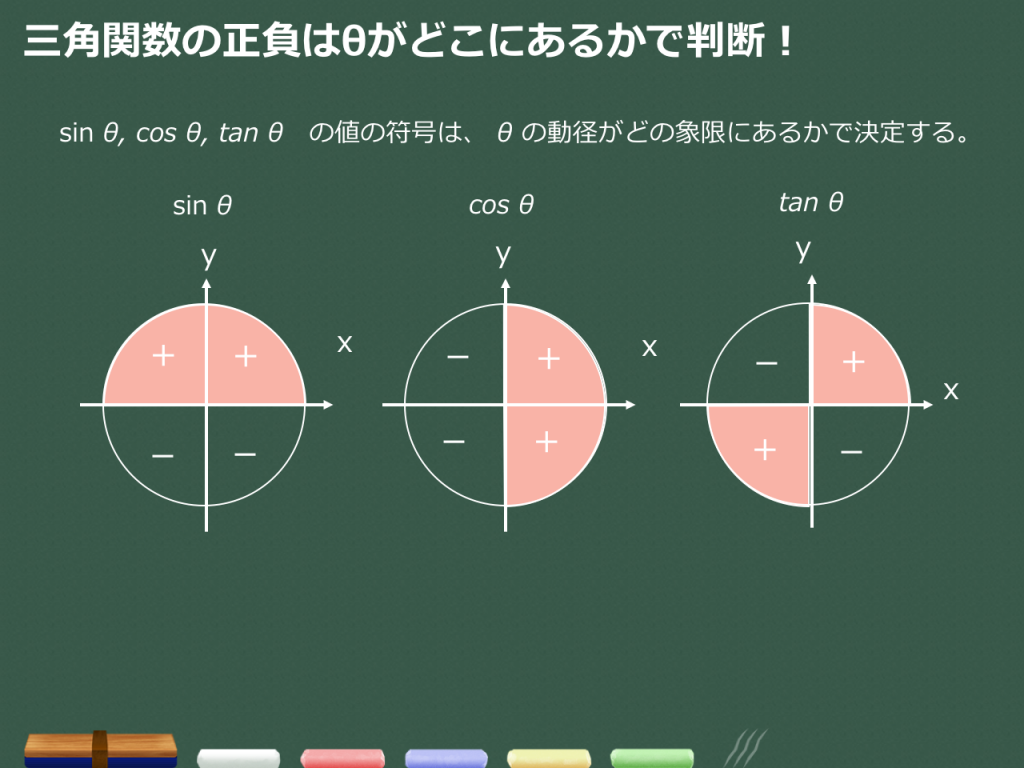
三角関数の象限ごとの符号は右の表のようになる。 これは、sin はy 座標、cos はx 座標、tan は直線の傾き に着目することで判定することもできる。 三角関数の相互関係 単位円上で三角関数を考えた場合、三角関数はcos , sin , x y sin tan cos y x となる。三角関数の性質と相互関係の例題 θ と θ＋ ( π /2)の関係 sinθ＋cosθとsinθcosθの関係 sinθ＋cosθ、sinθcosθとsin^3θ十cos^3θ sinθ－cosθとsinθcosθの関係 sinθ－cosθ、sinθcosθとsin^3θ－cos^3θ 三角関数の相互関係を用いる証明 三平方の定理による三角関数の計算（1） 三平方の定理による三角関数の計算（2）10．三角関数｜1．定義と基本性質｜3．三角関数の基本性質｜1．三角関数の相互関係 2/3 （例） が第4象限の角で、 5 1 cos が成り立つとき、sin 、tan の値を求める。 sin2 cos2 1より 1

Tossランド 三角関数の相互関係

8が第3象限の角で Cos8 13 12のとき 三角関数の Yahoo 知恵袋

三角比の相互関係は三角関数の基本であることを忘れないでください。 直線の傾きとタンジェント \(\,2\,\)本の直線のなす角は三角関数になりますので、 ここでは原点を通る直線の傾きと\(\,x\,\)軸となす角をタンジェントで表しておきます。 一般に、数学b/三角関数 3 / 32 角と象限 座標平面上で，x 軸の正の部分を始線とする角µ の動径について 1 角µ の動径が第1 象限にあるとき，µ を第1象限の角という． 2 角µ の動径が第2 象限にあるとき，µ を第2象限の角という． 3 角µ の動径が第3 象限にあるとき，µ を第3象限の角という．三角関数 sin ⁡ θ, cos ⁡ θ, tan ⁡ θ \sin\theta,\cos\theta,\tan\theta sin θ, cos θ, tan θ の間には，上記のような3つの関係式が成立します。 これらの関係式のことを， 三角関数の相互関係 と言います。 このページでは，三角関数の相互関係の証明を2通り解説します。

高2の数iiです 不等号の向きはどのような理由で変わるのか教えて欲しいです Clear

三角関数の値の正負 数学ii By Okボーイ マナペディア

次の問いを通して，三角比の相互関係を考えるよ 1 次の問いに答えよう (1) \(0° \leqq \theta \leqq 180°\) で \(\displaystyle \sin\theta = \frac{3}{5}\) を満たすとき，\(\cos\theta\) と \(\tan\theta\) の値は？ (2) \(\theta\) が第2象限の角で \(\tan\theta = 2\) を満たすとき，\(\sin\theta\) と \(\cos\theta\) の値は？ 2 \(0° \leqq \theta \leqq 180°\) で定義された関数 三角関数の相互関係 基本三角比の相互関係や基本三角比の相互関係（鈍角）で見たように、 $\sin$, $\cos$, $\tan$ は、それぞれ、関係式によって結びついていました。今までは、0度から180度の場合で考えていましたが、一般の角度に対しても成り立ちます。三角関数との関係で言えば，象限ということを意識しないと，符号の決め方が分からなくなるはずです． 例えば， において x, y は象限に応じて決まる符号が付いていて（符号付の実数）， r だけは半径（長さ，符号なしの実数）なので常に正です．

三角関数の符号と動径の象限 数学ii フリー教材開発コミュニティ Ftext

1番最後の意味を教えてください Clear

三角関数の象限ごとの符号は右の表のようになる。 これは、sin はy 座標、cos はx 座標、tan は直線の傾き に着目することで判定することもできる。 三角関数の相互関係 単位円上で三角関数を考えた場合、三角関数は cos , sin , x yこの問いは，上で導いた 三角関数の相互関係 を用いて式により求める方法と，図を描いて求める方法とがあります。 解答1 cosθ = − 4 5 を sin2θ cos2θ = 1 に代入します。 sin2θ ( − 4 5)2 = 1 sin2θ = 1 − 16 25 sin2θ = 9 25 θ は第3象限の角だから sinθ < 0 ∴ sinθ = − 3 5 sinθ = − 3 5 と cosθ = − 4 5 を tanθ = sinθ cosθ に代入して tanθ = − 3 5 − 4 5 = 3 4 以上より sinθ = − 2．三角関数と象限の関係 三角関数と正弦曲線の関係の説明をする際に、横軸x、縦軸yとした時の原点を中心に単位円を描いて考えていきました。 なので、三角関数にも象限は関係してきます。 関係するといっても、象限に応じて符号が変化するだけですけどね。

Http Www Shukutoku Ed Jp Wp Wp Content Uploads 04 Dbafee3606da87fce575e446 Pdf

3

 三角関数の復習 θ = x, tan = y x となるのでした（ x = 0 x = 0 のとき、 tan tan は定義しない）。 これにより、いろんな角に対して三角関数を定義することができるようになりましたが、より考えやすい角の三角関数に変換することができます。 以下で、その三角関数の相互関係式 象限ごとに、符 号が変わるので 注意しておこう!!三角関数の相互関係2の解答 氏名 1 ABCについて、次の問いに答えよ。 （1）cosθ = 3 4 のとき、sinθ、tanθの値を求めよ

三角関数 3 が全くわかりません 解説お願いしたいです よろしくお願いします Clear

高1数学a 三角比の相互関係 なぜマイナスをつけるのかがわかりません 高校 教えて Goo

三角関数の相互関係 数学Ⅰで、三角比の相互関係について学習しましたが、三角関数でもまったく同じ公式を使います。 ー① ー② ー③ 練習問題1 θが第3象限の角で、 のとき、cosθとtanθの値を求めなさい。 「θが第3象限の角」と三角関数（三角比）の相互関係 関係式 sin 2 θ cos 2 θ = 1 ⇒ 証明 tan θ = sin θ cos θ （ただし， cos θ ≠ 0 ） ⇒ 証明 tan 2 θ 1 = 1 cos 2 θ （ただし， cos θ ≠ 0 ） ⇒ 証明 ここも参考にするとよい． 証明 1．三角関数の定義より（右図参照）， sin θ = y r ， cos三角関数の相互関係 すべて覚えておいた方がよい公式です。 sin ⁡ 2 θ cos ⁡ 2 θ = 1 \sin^2\theta\cos^2\theta=1 sin 2 θ cos 2 θ = 1

三角関数の相互関係 数学板書

三角比と三角関数の公式の整理と歴史的背景 単元まとめ ますだ先生の数学の授業で自由に楽しむサイト

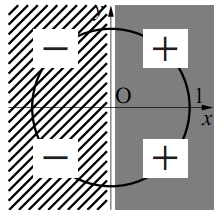
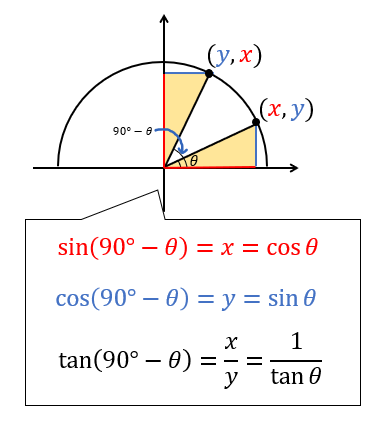
←拡張された三角関数の相互関係 ここで，$\pi {\theta}2\pi,~\tan{\theta}>0$より$\theta$は第$3$象限の角に対応し，$\cos\theta 0$． よって，$\boldsymbol{\cos{\theta}=\dfrac{1}{\sqrt{5}}}$．また，$\sin{\theta} =\tan{\theta}\cos{\theta}=2\times \dfrac{1}{\sqrt{5}}=\boldsymbol{\dfrac{2}{\sqrt{5}}}$．①三角関数部分 ②符号 角度がどこの象限にあるかを調べ、その符号を適用させる。 θなどの文字を含んでいる場合はθを第1象限の角(6 など)と 仮定して元の三角関数に代入し、 6 2 n がどこの象限にあるかを調べ、 その符号を適用させる。 例） 8 7 7 7π=180°を足すと、第1象限 第3象限 角度がθの直角三角形を図に示し、θπがどの位置に移るのか考えてみましょう。 角度θの直角三角形アが第1象限にあったとします。 θπということは、ここから更に π=180° 移動した場所に直角三角形が来ることを表しています。 第3象限 に移動してイの三角形になりますね。 このイの直角三角形に注目しましょう。 cos (θ＋π)の

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

11 E 2 Sin 0 Dfrac 1 Descubre Como Resolverlo En Qanda

41 三角関数 135 一般に，次のことがいえる．ただし，nは整数である． ¶ ‡ 動径OP と始線OX のなす角の1 つをfi とすると，動径OP の表す角 はfi 360 £ n である． µ 練習42 次の角のうち，その動径が60– の動径と同じ位置にある角はどれか． 300– ，4– 1040– ¡60–，¡300–，¡780–三角関数の相互関係の式である、 sin2θ cos2 θ = 1 sin 2 θ cos 2 θ = 1三角関数の相互関係 (21) ここで，は原点を中心とする半径の円周上の点だから，が成り立つ．よって (22) ※以下においては，角として第1象限の角を使って解説しますが，求めた結果はがどのような角とかの場合でも成り立ちます． 第1象限の角として解説するのは，符号や長さが見た目のままになり「分かりやすい」からです． 偶関数，奇関数の関係 (23

基本 三角関数の相互関係 なかけんの数学ノート

数学 Ii 第1節 三角関数 三角関数 B 三角関数の相互関係 画像右 例題 8の動径が第４象限にあり Sin8 1 3のとき Cos8tan8の値をを それぞれ求めよ

Tan = sin cos ;Sin,cos,tanのどれがわかっているかで使う三角形が決まります。 アの三角形を使う場合 三角形は 斜辺と高さ がわかっていますね sin がわかっている時に使います。 イの三角形を使う場合 三角形は 斜辺と底辺 がわかっていますね cos がわかっている時に使います。 ウの三角形を使う場合 三角形は 底辺と高さ がわかっていますね数II三角関数三角関数の相互関係 第2象限ではcosθの符号は負 cos 2 θ=1sin 2 θ=14/9=5/9 の平方根の負の方を答えます。

数学について質問です なぜsinaなのに Aの動径は第1象限 Yahoo 知恵袋

数学 Ii Yvmfz7d6a1tmvov تويتر

三角関数 MathAquarium例題三角関数 1 Oxx yy Ox y 第2象限 第1象限 第3象限象限第4 三角関数 1動径の表す角（角の図示，第〇象限） 点O を原点とする座標平面において，x軸の正の部分を始線にとり，次の角だけ回転した動径OP を図示 せよ。 また，動径OP の表す一般角θを，θ＝α＋360° ×n（0°≦α＜360°，nは整数）の形で表し， 第何象限の角か答えよ。 (1) 500° (2Tan = sin cos で sin を消去したものです。1三角関数の相互関係の特徴 2角の象限と三角関数の値の符号 3三角関数の相互関係の公式を利用する注意点 学習メモ 理解度チェック 三角

Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data 2 319 2 Shinsugaku 319 2 Kyoukashoword 319 2 Kyoukashoword 3 1 Pdf

2講 三角関数 1節 三角関数 問題集 4章 三角関数 中学生 小学生 高校生のテストや受験対策に おすすめ無料学習問題集 教材サイト

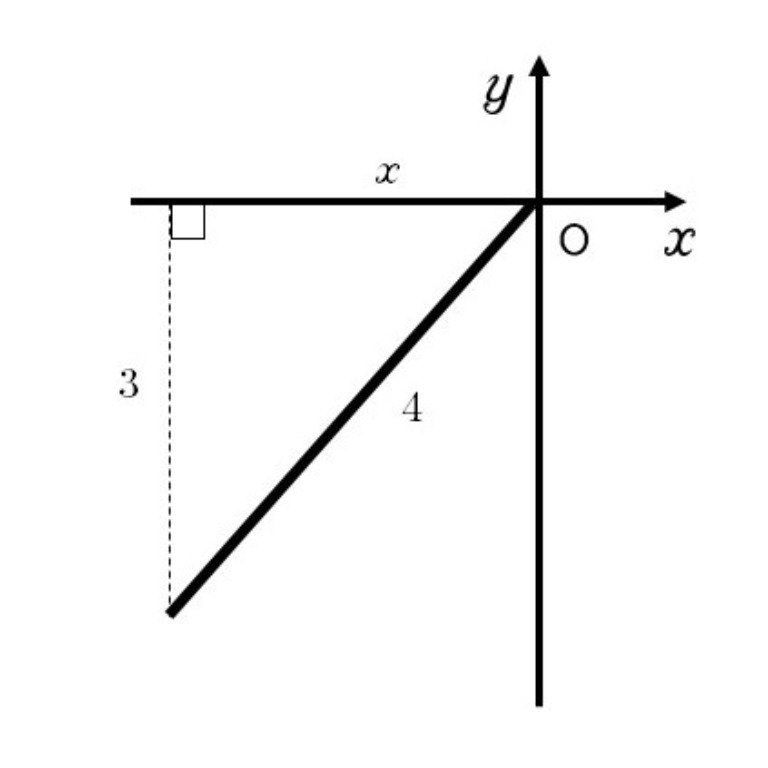
まずは解法1、三角関数の相互関係を使って求めていきます。三角形の相互関係とは以 下の通りです。 三角関数の相互関係 sin2 cos2 = 1;三角関数の相互関係 ⑴ tanθ = sinθ cosθ ⑵ sin2 θ cos2 θ = 1 (sinθ)2 (cosθ)2 = 1 のことです ※上の式を使って解く方法よりも、図を描いて解く方法のほうが簡単だと思います。 例1 θ が第3 象限の角度で、sinθ = − 2 3 のときcosθ とtanθ を求めよ。 解答 右のようより、 なので となる。 より、 より、 sin𝜃=− 3 4 cos𝜃tan𝜃 𝒊 𝜽𝒄 𝜽= 𝑐 𝑠2𝜃=1−𝑠𝑖 2𝜃 𝑐

座標平面 第１象限 第２象限 第３象限 第４象限 一夜漬け高校数学436 図形と方程式 数学 Youtube

12月6日 藤２勤数

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

三角関数の相互関係 高校数学の無料オンライン学習サイトko Su

Http Www Shukutoku Ed Jp Wp Wp Content Uploads 04 Dbafee3606da87fce575e446 Pdf

なんで第3象限とかってわかるんですか Cos8の第２象限第３象限の見分け方 Clear

三角関数 3 が全くわかりません 解説お願いしたいです よろしくお願いします Clear

基礎から学ぶ三角関数 三角関数と象限 角度と符号の関係 ふらっつのメモ帳

基礎から学ぶ三角関数 三角関数と象限 角度と符号の関係 ふらっつのメモ帳

21年大学入試共通テスト 数学ia 第1問 2 図形 三角比 余弦定理 正弦定理など 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

4 0 3 Key 69 12 1 1 Lihat Cara Penyelesaian Di Qanda

Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data 2 317 2 Advanced 317 2 Kyoukashoword 317 2 Kyoukashoword 3 1 Pdf

2

高校数学 Sin8とcos8を解にもつ2次方程式 Sin8とcos8の連立方程式 受験の月

Sin Cos Tanの相互関係

3 Sine Tan 0 100 Cosesin Descubre Como Resolverlo En Qanda

三角関数の値 定義 I

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

数ii三角関数三角関数の相互関係8の動経が第2象限にあり Sin8 1 5 Yahoo 知恵袋

数1三角比 こういう問題ってどうして範囲が決められているのですか Clear

三角関数の符号と動径の象限 数学ii フリー教材開発コミュニティ Ftext

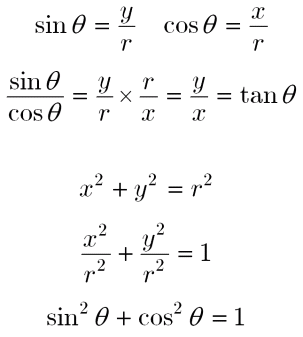
三角比 三角関数の相互関係と 象限 大人が学び直す数学

3分で分かる 三角関数の基礎知識 合格サプリ

メルカリ 苦手克服シリーズ 数学 参考書 500 中古や未使用のフリマ

Http Www Educ Pref Fukuoka Jp Static E5 Ad A6 E6 A0 A1 E6 94 Af E6 8f B4 E4 Ba 8b E6 A5 Ad 86 84 Ef 97 Up 1sl6wd5y E6 95 B0 E5 Ad A6 E2 85 A1 81 Ae E5 9f Ba E6 9c Ac E2 91 A3 Ef E4 B8 E8 92 E9 96 E6 95 B0 Ef Ef Bf E8 A3 E7 Ad 94 E4 98 Pdf

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data 2 319 2 Shinsugaku 319 2 Worksheet 319 2 Work 3 1 Pdf

高校数学 三角関数の相互関係と還元公式 負角の公式 補角の公式 余角の公式 受験の月

Www2 Osaka C Ed Jp Blog Momodani C Blog Name F0fa40eeb1caaf567e013ced8b Pdf

高校数学 の問題集 三角関数 のところで 鋭角の三角関数で表しなさい と Yahoo 知恵袋

三角関数

三角比の相互関係

基本 三角関数の相互関係 なかけんの数学ノート

高校数学 弧度法表示の三角関数 Cos8編 映像授業のtry It トライイット

高校数学の三角関数sin Cos Tanの各象限の符号をどん Yahoo 知恵袋

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data 2 319 2 Shinsugaku 319 2 Kyoukashoword 319 2 Kyoukashoword 3 1 Pdf

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

三角関数の相互関係の公式を使った練習問題 数学ii By ふぇるまー マナペディア

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

高校数学 8 と 8 P 8 Pの関係 映像授業のtry It トライイット

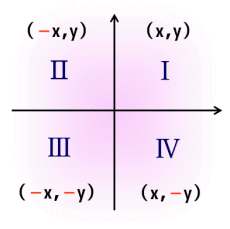
三角比 三角関数の相互関係と 象限 大人が学び直す数学

高校数学 三平方の定理による三角関数の計算 １ 映像授業のtry It トライイット

三角関数の相互関係 Geogebra

三角関数の相互関係 Geogebra

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

高校数学 三角関数tan8の不等式 映像授業のtry It トライイット

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

高校数学 8 と 8 P 8 Pの関係 映像授業のtry It トライイット

基礎から学ぶ三角関数 三角関数と象限 角度と符号の関係 ふらっつのメモ帳

基本 三角関数の相互関係 なかけんの数学ノート

Http Web Math Aquarium Jp Reidai Sannkakukannsuu Pdf

三角比 三角関数の相互関係と 象限 大人が学び直す数学

高校数学の三角関数sin Cos Tanの各象限の符号をどん Yahoo 知恵袋

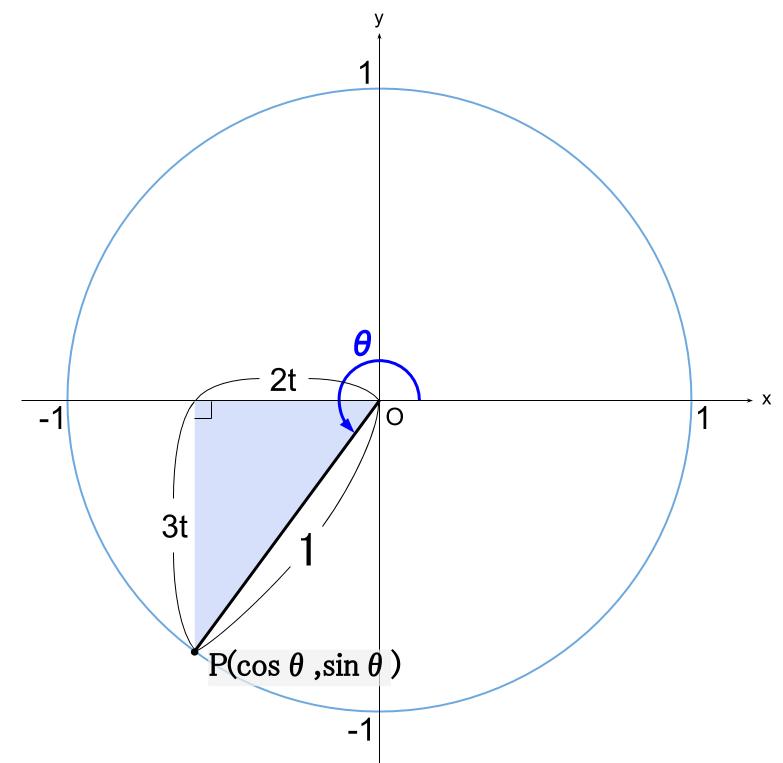
三角関数の相互関係 高校数学の無料オンライン学習サイトko Su

Www Kyokyo U Ac Jp Cece 2 3 Pdf

一夜漬け高校数学16 三角関数 相互関係 練習問題 Cos8 Youtube

2

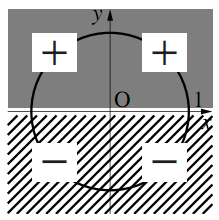
三角関数の符号と動径の象限 数学ii フリー教材開発コミュニティ Ftext

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

0 8 180 のときの三角比のまとめ 数学i By Okボーイ マナペディア

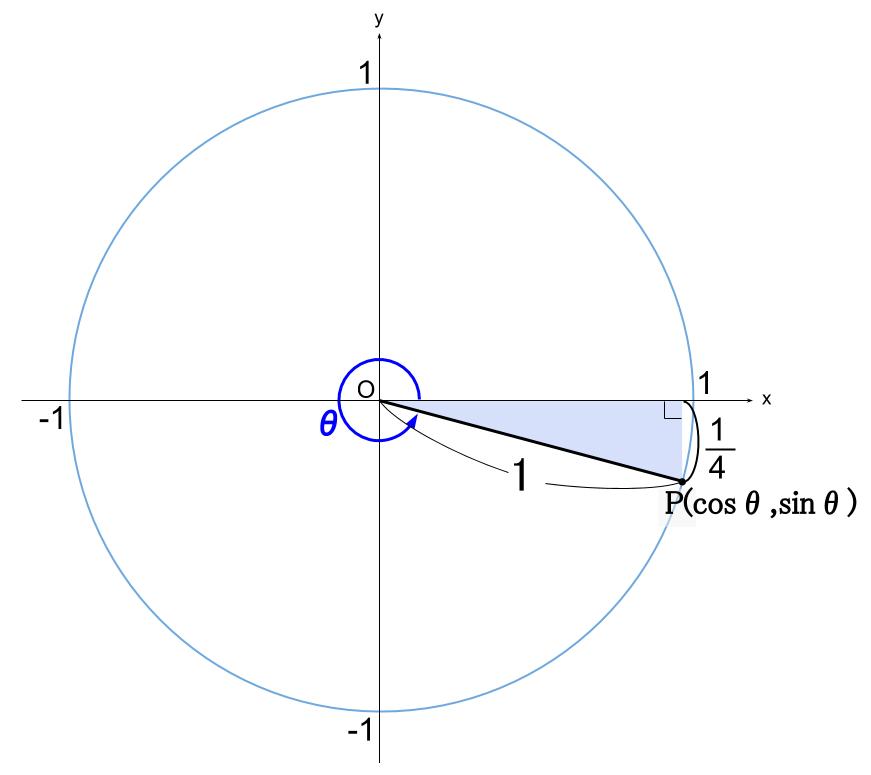
三角関数の相互関係 高校数学の無料オンライン学習サイトko Su

Http Www Educ Pref Fukuoka Jp Static E5 Ad A6 E6 A0 A1 E6 94 Af E6 8f B4 E4 Ba 8b E6 A5 Ad 86 84 Ef 97 Up O0jvwtlu E6 95 B0 E5 Ad A6 E2 85 A1 81 Ae E5 9f Ba E6 9c Ac E2 91 A3 Ef E4 B8 E8 92 E9 96 E6 95 B0 Ef Pdf

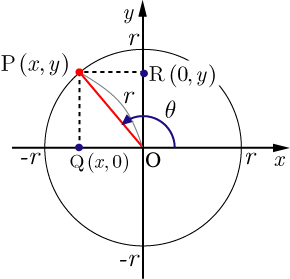
三角関数の相互関係

3

Http Www Educ Pref Fukuoka Jp Static E5 Ad A6 E6 A0 A1 E6 94 Af E6 8f B4 E4 Ba 8b E6 A5 Ad 86 84 Ef 97 Up O0jvwtlu E6 95 B0 E5 Ad A6 E2 85 A1 81 Ae E5 9f Ba E6 9c Ac E2 91 A3 Ef E4 B8 E8 92 E9 96 E6 95 B0 Ef Pdf

三角関数の相互関係の公式を使った練習問題 数学ii By ふぇるまー マナペディア

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

高校数学 三角関数の相互関係を用いる証明 映像授業のtry It トライイット

数学 Ii Pa Twitter 第1節 三角関数 三角関数 B 三角関数の相互関係 画像右 例題 8の動径が第４象限にあり Sin8 1 3のとき Cos8tan8の値をを それぞれ求めよ

三角関数の相互関係の問を教えて下さい 8が第4象限の Yahoo 知恵袋

三角関数の値の符号 一夜漬け高校数学277 Sin8 Cos8 Tan8 Youtube

高校数学 三角方程式 不等式 基本形 受験の月

Http Www Educ Pref Fukuoka Jp Static E5 Ad A6 E6 A0 A1 E6 94 Af E6 8f B4 E4 Ba 8b E6 A5 Ad 86 84 Ef 97 Up O0jvwtlu E6 95 B0 E5 Ad A6 E2 85 A1 81 Ae E5 9f Ba E6 9c Ac E2 91 A3 Ef E4 B8 E8 92 E9 96 E6 95 B0 Ef Pdf

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

この2問を教えてください Clear

数学 Ii Pa Twitter 第1節 三角関数 三角関数 B 三角関数の相互関係 画像右 例題 8の動径が第４象限にあり Sin8 1 3のとき Cos8tan8の値をを それぞれ求めよ

三角比の拡張 第2象限の角 1 鈍角 一夜漬け高校数学9 Youtube

1

Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data 2 319 2 Shinsugaku 319 2 Kyoukashoword 319 2 Kyoukashoword 3 1 Pdf

数学i Aチェック リピート 第4章 1三角比 2 鈍角の三角比 相互関係 Pukiwiki